2) Второе ограничение связано с формой распределения величины фиксированных описанными выше шкалами, которое предполагается нормальным. Для нормального распределения оценки меры рассеяния совпадают: Мо=Ме=М, в скошенном хвосты распределения не влияют на среднюю (М).
Таким образом, необходимо внимательно изучать форму распределения с точки зрения его отклонения от нормального.
II
. Используя понятия интегральной функции распределения и определенного интеграла можно записать
¦
(
x
) =
F
¢
(
x
) или
F
(
x
) =
p
(
x
1
<
X
<
x
2
) =
.
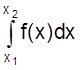
Если 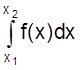определяет заштрихованную область в соответствующих пределах, то
p (х
<
Х
<
х
+
D
х)
»
¦
(х)
D
х.
Это соотношение можно представить в виде простого геометрического толкования для каждого класса.
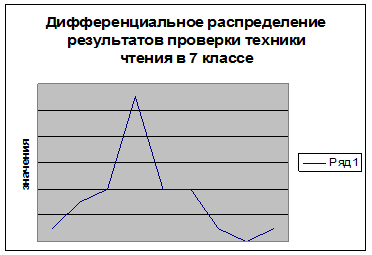
Рис. 1 График дифференциального распределения результатов проверки техники чтения в 7 классе
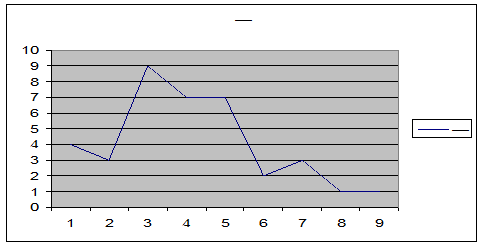
Рис. 2 Результаты дифференциального распределения результатов проверки техники чтения в 8 классе
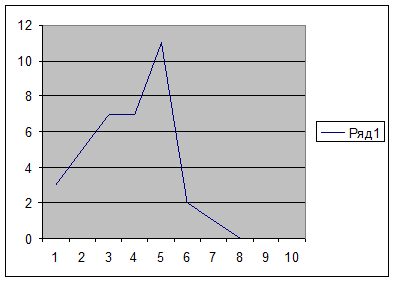
Рис. 3 Результаты дифференциального распределения результатов проверки техники чтения в 9 классе.
Для дискретной случайной величины справедливо следующее равенство:
F
(
x
) =
P
(
X
<
x
) =
P
(
-
¥
<
X
<
x
) =
,
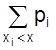
где суммирование распространяется на х
i
<
х.
В промежутке между двумя последовательными значениями Х функция
F
(х) постоянна. При переходе аргумента х через значение х
i
F
(х) скачком возрастает на величину p (Х
=
х
i
).
Рассмотрим p (х1
£
Х
<
х2). Если х2
>
х1, то очевидно, что
p (Х
<
х2)
=
p (Х
<
х1)
+
p (х1
£
Х
<
х2).
Тогда
p (х1
£
Х
<
х2)
=
p (Х
<
х2)
-
p (Х
<
х1)
=
F
(х2)
-
F
(х1),
т.е. вероятность попадания случайной величины в интервал
[
х1
;
х2) равен разности значений интегральной функции граничных точек.
Последнее условие можно использовать для нахождения вероятности p (Х
=
х1) для непрерывной случайной величины. Для этого рассмотрим предел
p
(
X
=
x
1
) =
,
т.е. если закон распределения случайной величины есть функция непрерывная, то вероятность того, что случайная величина примет заранее заданное значение, равна нулю.
Здесь видно различие между дискретными и непрерывными случайными величинами. Для дискретных случайных величин, для каждого значения случайной величины существует своя вероятность. И для него справедливо утверждение: событие, вероятность которого равна нулю, невозможно. Для непрерывной случайной величины это утверждение неверно. Как показано, вероятность того, что Х
Как вы относитесь к деньгам?
Деньги на протяжении всей человеческой истории были причиной войн, священные писания обвиняли их в развращении человеческой души, и так или иначе большинство преступлений совершается именно из-за них. Деньги — сильнейший стимул. И многие люди не могут устоять перед искушением их заполучить.
Независимо от нашего экономического положения ...
Психологические основы социальной реабилитации
Выше отмечалось, что очень часто алкоголизм и прочие аддиктивные проблемы становятся семейной традицией. Более пятидесяти процентов сегодняшних алкоголиков являются детьми алкоголиков, кроме того, у миллионов людей имеются иные серьёзные проблемы. Очень важно уберечь детей от мучительных лет молчания, стыда, страданий. Социальные работн ...
Память
Памятью называют нашу способность припоминать прошлые события, поступки, людей, объекты, ситуации, усвоенные навыки и т. д. Она также имеет отношение к тому, как мы храним подобную информацию. В соответствии с классификацией Р.Аткинсона и Р.Шифрина, различают три подтипа памяти и связанных с ней процессов: 1) сенсорную помять, первичное ...